Số nguyên là khái niệm toán học trong chương trình giáo dục của Việt Nam. Tuy nhiên, nhiều người vẫn chưa hiểu rõ số nguyên là gì cũng như đặc điểm và ứng dụng của nó trong toán học. Hãy cùng tìm hiểu ngay trong bài viết dưới đây!
1. Số nguyên là gì?
Số nguyên là tập hợp các số bao gồm số 0, số tự nhiên (lớn hơn 0) và số đối của nó (nhỏ hơn 0). Tập hợp số nguyên là vô hạn, đếm được và ký hiệu là Z. Như vậy, nếu chưa biết Z là tập hợp số gì thì đó chính là các số nguyên.

2. Phân loại số nguyên
Trong toán học, số nguyên được chia thành hai loại là số nguyên dương và số nguyên âm. Cụ thể:
2.1. Số nguyên dương là gì?
Số nguyên dương (ký hiệu Z+) là số lớn hơn 0 và không có phần thập phân. Nói cách khác, số nguyên dương chính là N. Vậy N là tập hợp số gì? N là tập hợp các số tự nhiên.
Ví dụ: Số 1, 2, 3, 4, 5,... lớn hơn 0 nên là số nguyên dương.
2.2. Số nguyên âm là gì?
Số nguyên âm (ký hiệu Z-) là số nhỏ hơn 0 và không có phần thập phân.
Ví dụ: Số -1, -2, -3, -4, -5,... nhỏ hơn 0 nên là số nguyên âm.
Xem thêm: Số nguyên tố là gì? Bảng số nguyên tố toán học, kèm ví dụ chi tiết3. Đặc điểm của số nguyên
Số nguyên có các đặc điểm sau đây:
Tập hợp các số nguyên là vô hạn nên không thể xác định được số nguyên âm nhỏ nhất và số nguyên dương lớn nhất.
Số nguyên dương nhỏ nhất là 1 và số nguyên âm lớn nhất là -1.
Tập hợp số nguyên bao gồm các tập con hữu hạn. Bạn có thể xác định được số nguyên nhỏ nhất và lớn nhất trong tập con hữu hạn đó.
Không có số nguyên nào nằm giữa hai số nguyên liên tiếp.
Tổng của hai số nguyên bất kì luôn là một số nguyên.
Thứ tự của các số hạng không ảnh hưởng đến kết quả phép cộng và phép nhân các số nguyên.
Việc nhóm các số hạng không ảnh hưởng đến kết quả phép cộng và phép nhân các số nguyên.
4. Tập hợp và cách biểu diễn của số nguyên
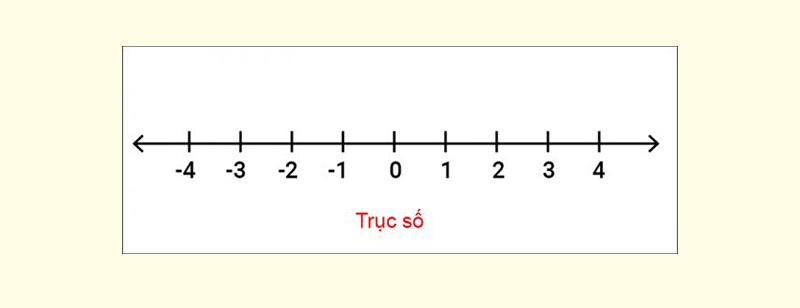
Số nguyên kí hiệu là gì? Tập hợp các số nguyên được ký hiệu là Z. Trên trục số, số 0 nằm giữa, số nguyên dương nằm bên phải, số nguyên âm nằm bên trái và tất cả được biểu diễn cách đều nhau. Cách biểu diễn này giúp hiểu rõ hơn về vị trí và mối quan hệ của tập hợp các số nguyên. Từ đó, học sinh có thể dễ dàng giải các bài toán liên quan đến cộng, trừ, so sánh,...
5. Một số bài tập vận dụng số nguyên
Để hiểu hơn về số nguyên là những số nào, bạn có thể tham khảo các bài toán dưới đây:
Bài tập 1: Các phát biểu dưới đây là đúng hay sai:
a) 20 ∈ Z
b) -40 ∉ Z
- Cách giải:
a) 20 ∈ Z
20 là số nguyên dương nên phát biểu này đúng.
b) -40 ∉ Z
-40 là số nguyên âm nên phát biểu này sai.
Bài tập 2: Tìm các số đối của các số sau: 10, 24, -35, 44 và -58.
Cách giải:
Số đối của số 10 là -10
Số đối của số 24 là -24
Số đối của số -35 là 35
Số đối của số 44 là -44
Số đối của số -58 là 58
Bài tập 3: Sắp xếp các số nguyên sau đây theo thứ tự tăng dần: 20, -10, 3, -5, -9, 30
Cách giải:
Các số nguyên sắp xếp theo thứ tự tăng dần như sau: -10, -9, -5, 3, 20, 30.
Bài tập 4: Cho tập hợp A = {2, 5, -7, -9, 13}
a) Viết tập hợp B gồm A và các số đối của chúng.
b) Viết tập hợp C gồm các phần tử lớn hơn các phần tử của B 1 đơn vị.
Cách giải:
a) Tập hợp B = {-2, -5, 7, 9, -13}
b) Tập hợp C = {-1, -4, 8, 10, -12}
Xem thêm: Số hữu tỉ là gì? Các phép toán với số hữu tỉ kèm bài tập chi tiết6. Ứng dụng của số nguyên trong toán học
Sau khi hiểu rõ số nguyên là gì, khái niệm này được ứng dụng nhiều trong toán học, cụ thể như sau:
6.1. Bài toán cơ bản với số nguyên
Số nguyên được ứng dụng để học sinh làm quen với toán học qua phép cộng, trừ, nhân, chia. Ví dụ như:
Phép cộng: Hai số nguyên âm hoặc nguyên dương cộng lại với nhau.
Ví dụ: 3 + 4 = 7 hoặc (-3) + (-4) = -7
Phép trừ: Lấy số nguyên này trừ đi số nguyên khác.
Ví dụ: 8 - 5 = 3 hoặc (-5) - (-8) = 3
Phép nhân: Nhân hai số nguyên với nhau.
Ví dụ: 3 x (-5) = -15 hoặc 3 x 4 = 12
Phép chia: Lấy số nguyên này chia cho số nguyên khác. Phép chia các số nguyên có thể dư nên không phải lúc nào kết quả cũng cho ra số nguyên.
Ví dụ: 12 : 3 = 4 hoặc (-18) : 6 = (-3)
6.2. Số nguyên trong hình học
Số nguyên được dùng để tính góc, đoạn thẳng và diện tích trong các bài toán hình học. Bên cạnh đó, số nguyên giúp học sinh xác định tọa độ một điểm trên mặt phẳng của hình học tọa độ. Ngoài ra, số nguyên còn biểu thị khoảng cách giữa các điểm hoặc tọa độ các vector.
6.3. Số nguyên trong xác suất và thống kê
Số nguyên được ứng dụng trong các bài toán xác suất và thống kê khi đếm số lượng sự kiện hoặc số lượng kết quả. Thêm nữa, số nguyên được sử dụng để tính toán các đại lượng trong bài toán thống kê như phương sai, độ lệch chuẩn, trung bình,...
7. Ứng dụng của số nguyên trong đời sống thực tế
Ứng dụng trong đời sống thực tế của số nguyên là gì? Số nguyên được ứng dụng trong một số lĩnh vực sau đây:
7.1. Trong khoa học và kỹ thuật
Số nguyên thường được dùng để thể hiện các giá trị trong khoa học và kỹ thuật như kích thước, số lượng, đơn vị đo lường,... Ngoài ra, số nguyên còn là một dữ liệu trong lập trình máy tính giúp thực hiện các phép toán, xây dựng thuật toán cũng như lưu trữ dữ liệu.
7.2. Trong kinh tế và tài chính
Trong kinh tế và tài chính, số nguyên dùng để tính toán lãi suất, lợi nhuận, các khoản vay nợ,… Ngoài ra, các kế toán còn dùng số nguyên để ghi chép và theo dõi các giao dịch, từ đó quản lý tài chính cho công ty hiệu quả hơn.

Bài viết trên đã giải đáp số nguyên là gì, đặc điểm cùng những bài toán liên quan đến những con số này. Việc hiểu rõ số nguyên không chỉ giúp nâng cao kết quả học tập mà còn có thể ứng dụng trong nhiều lĩnh vực đời sống.
CHƯƠNG TRÌNH KHUYẾN MÃI LỚN TẠI ĐIỆN MÁY CHỢ LỚN! Càng gần cuối năm, Trang Công Nghệ càng tổ chức nhiều chương trình khuyến mãi hấp dẫn, giảm giá sâu cho các sản phẩm nội thất, đồ gia dụng, điện tử,... cùng nhiều quà tặng giá trị cao. Bên cạnh đó, khách hàng không cần lo lắng về chi phí mua hàng bởi nơi đây cam kết mức giá rẻ nhất thị trường, hỗ trợ trả góp 0% lãi suất và trả trước 0 đồng qua các công ty tài chính. > Nhanh chóng đến với địa chỉ gần nhất hoặc liên hệ hotline để được tư vấn tận tình nhé! |



![[Giải đáp] Còn bao nhiêu ngày nữa đến Tết Nguyên Đán 2025?](http://cdn.trangcongnghe.vn/thumb/160x240/2024-10/gii-ap-con-bao-nhieu-ngay-na-n-tt-nguyen-an-2025-1.jpg)