Hợp số không chỉ là kiến thức toán học mà còn giúp bạn ứng dụng trong thực tiễn. Vậy hợp số là gì? Chúng có đặc điểm và ứng dụng ra sao? Bài viết dưới đây sẽ giải đáp chi tiết nhất để bạn hiểu rõ về hợp số!
1. Số nguyên tố và hợp số là gì?
Trong toán học, số nguyên tố là số tự nhiên lớn hơn 1, đồng thời có hai ước duy nhất bao gồm số 1 và chính nó. Ví dụ: Số 3 có hai ước bao gồm số 1 và số 3 nên được gọi là số nguyên tố.
Vậy thế nào là hợp số? Hợp số là số tự nhiên lớn hơn 1 và có nhiều hơn hai ước. Ví dụ: Số 6 có bốn ước bao gồm số 1, số 2, số 3 và số 6 nên được gọi là hợp số.
Lưu ý:
Số 1 và số 0 không phải là hợp số, cũng không nằm trong nhóm số nguyên tố.
Tất cả các số tự nhiên lớn hơn 1 đều có nhiều hơn 1 ước số.
Số 2 là số nguyên tố nhỏ nhất, đồng thời là số nguyên tố chẵn duy nhất.
Các số nguyên tố ngoài số 2 đều là số lẻ nhưng không phải số lẻ nào cũng là số nguyên tố.
Cách kiểm tra số nguyên tố là tìm tập hợp các ước của nó.
Tổng hợp các loại hợp số Có hai loại hợp số đó là Hợp số lẻ và Hợp số chẵn. Trong đó:
|
Xem thêm: Số nguyên tố là gì? Bảng số nguyên tố toán học, kèm ví dụ chi tiết
2. Đặc điểm của hợp số
Hợp số là những số có các đặc điểm sau đây:
Hợp số là tất cả các số tự nhiên lớn hơn 1 và không phải số nguyên tố.
Có vô số các hợp số.
Hợp số có ít nhất 1 ước số là số nguyên tố nhỏ hơn căn bậc hai của chính số.
Hai hợp số đều có ít nhất một ước chung là số 1.
Tích của hai số nguyên tố là một hợp số.

3. Hướng dẫn cách tìm hợp số đơn giản, nhanh chóng
Nếu chưa biết cách tìm hợp số là gì thì bạn chỉ cần thực hiện theo một trong ba hướng dẫn sau:
3.1. Phương pháp 1:
Đầu tiên, bạn có thể áp dụng phương pháp lặp từng phần tử với bước nhảy 1. Gọi N là số cần kiểm tra, cách thực hiện như sau:
Bước 1: Nhập số N.
Bước 2: Nếu N bé hơn 2 thì không phải hợp số. Nếu N lớn hơn 2 thì tiếp tục thực hiện bước 3.
Bước 3: Trong khoảng từ 2 đến (N-1), nếu xuất hiện số mà N chia hết thì N là hợp số. Nếu không, N là số nguyên tố.
Ví dụ: Để kiểm tra 14 có phải hợp số không, bạn tiến hành như sau:
Ta có 14 >2. Đồng thời, trong khoảng từ 2 - 13, số 14 chia hết cho số 2 và số 7. Do đó, 14 là hợp số.
3.2. Phương pháp 2:
Để kiểm tra một số có phải hợp số hay không, bạn có thể áp dụng theo dấu hiệu chia hết cho 2; 3; 5; 9. Cụ thể, nếu số đó chia hết cho 2; 3; 5 hoặc 9 thì có ít nhất 2 ước số.
Ví dụ: Số 100 chia hết cho 2 nên là hợp số.
3.3. Phương pháp 3:
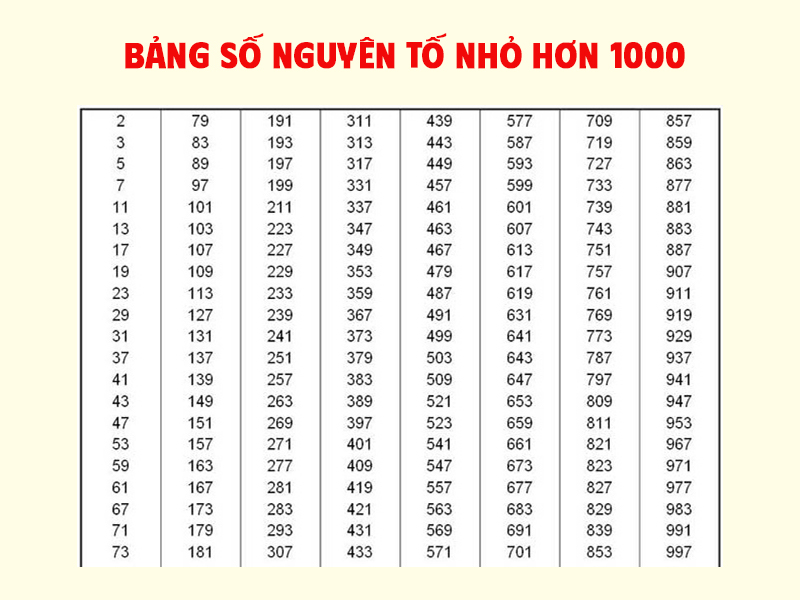
Ngoài hai cách trên, bạn có thể xác định hợp số dựa vào bảng tổng hợp các số nguyên tố. Nếu số đó không nằm trong bảng số nguyên tố thì chính là hợp số.
Ví dụ: Số 8 không nằm trong bảng số nguyên tố nên chính là hợp số. Số 5 thuộc bảng số nguyên tố nên không phải hợp số.
4. Ứng dụng của hợp số trong toán học và cuộc sống
Việc nắm được hợp số là những số nào giúp bạn ứng dụng trong bộ môn toán học và cả các tình huống thực tiễn trong cuộc sống. Cụ thể:
4.1. Ứng dụng trong mã hóa và bảo mật
Hợp số được dùng trong mã hóa - bảo mật để đảm bảo an toàn thông tin. Bởi quá trình phân tích hợp số thành thừa số nguyên tố cần nhiều thời gian và tài nguyên.
4.2. Ứng dụng trong số học
Trong số học, hợp số giúp học sinh hiểu rõ hơn về khái niệm chia hết. Bên cạnh đó, hợp số giúp bạn biết cách phân tích một số thành tích của các số nguyên tố. Đây là tiền đề để học sinh giải các bài toán phức tạp hơn, điển hình như tìm bội chung nhỏ nhất hoặc ước chung lớn nhất.
4.3. Ứng dụng trong lý thuyết số
Khái niệm hợp số là gì đóng vai trò quan trọng trong lý thuyết số. Cụ thể, việc phân loại hợp số và số nguyên tố giúp bạn hiểu rõ hơn về đặc điểm của tập hợp số tự nhiên. Ngoài ra, các bài toán liên quan đến hợp số như ước số, bội số,... là một phần quan trọng trong lý thuyết số.
4.4. Ứng dụng trong công nghệ máy tính
Việc phân tích hợp số thành thừa số nguyên tố được ứng dụng để phát triển thuật toán và chương trình máy tính. Điều này giúp nâng cao hiệu suất khi tìm ước số, bội số và thực hiện phép chia trong công nghệ máy tính.
4.5. Ứng dụng trong lập lịch và tổ chức công việc
Con người có thể phân tích hợp số để tìm ra bội chung nhỏ nhất của các chu kỳ, từ đó tìm ra khoảng thời gian hợp lý cho việc lặp lại các công việc khi lập lịch và tổ chức công việc. Điều này giúp nâng cao hiệu suất làm việc tốt hơn.

4.6. Ứng dụng trong vật lý và kỹ thuật
Hợp số được ứng dụng trong quá trình tính toán, xác định các hiện tượng có chu kỳ lặp lại hoặc thiết kế mô-đun. Việc phân tích hợp số thành các thành phần cơ bản hơn như thừa số nguyên tố sẽ giúp dễ dàng xác định tính chất, từ đó dự đoán hành vi của hệ thống vật lý và kỹ thuật.
4.7. Ứng dụng trong giáo dục
Trong giáo dục, hợp số giúp học sinh biết cách phân tích thừa số, phân loại số và giải các bài toán chia hết. Ngoài ra, một số bài toán hoặc câu đố liên quan đến hợp số giúp học sinh rèn luyện khả năng tư duy và giải quyết vấn đề trong quá trình học tập.

5. Một số bài tập về hợp số có cách giải chi tiết
Dưới đây là một số bài toán liên quan giúp bạn hiểu rõ về khái niệm hợp số:
5.1. Xác định hợp số
Đề bài: Xác định xem số 5, 9, 13 và 20 có phải hợp số hay không
Phân tích đề bài: Kiểm tra xem số đó có bao nhiêu ước số. Nếu có trên 2 ước số thì là hợp số. Nếu có hai ước số thì là số nguyên tố.
Cách giải:
Số 5 có 2 ước là số 1 và số 5. Do đó, số 5 là số nguyên tố.
Số 9 có 3 ước số là số 1, số 3 và số 9. Do đó, số 9 là hợp số.
Số 13 có 2 ước số là số 1 và số 13. Do đó, số 13 là số nguyên tố.
Số 20 có 5 ước số là số 1, số 2, số 4, số 5, số 10 và số 20. Do đó, số 20 là hợp số.
5.2. Phân tích hợp số thành thừa số nguyên tố
Đề bài: Phân tích số 30 thành thừa số nguyên tố.
Phân tích đề bài: Áp dụng phương pháp chia liên tiếp cho các số nguyên tố nhỏ hơn để phân tích hợp số đã cho.
Cách giải:
30 chia hết cho 2, ta có: 30 : 2 = 15
15 chia hết cho 3, ta có: 15 : 3 = 5
5 là số nguyên tố nên không chia được nữa.
Như vậy: 30 = 2 x 3 x 5
5.3. Tìm ước số của hợp số
Đề bài: Tìm ước số của hợp số 24.
Phân tích đề bài: Tìm các số mà hợp số đó chia hết. Ngoài ra, bạn có thể dựa vào phương pháp phân tích hợp số thành thừa số nguyên tố để giải bài toán tìm ước số.
Cách giải:
Phân tích 24 thành thừa số nguyên tố, ta có: 24 = 2^3 x 3
Các ước số là tích của các thừa số, từ 2^0, 2^1, 2^2, 2^3 và 3^0, 3^1.
Như vậy, tập hợp các ước số của hợp số 24 bao gồm: 1, 2, 3, 4, 6, 8, 12, 24.
5.4. Tìm các hợp số trong một khoảng cho trước
Đề bài: Tìm các hợp số nằm trong khoảng từ 5 đến 10
Phân tích đề bài: Kiểm tra từng số trong khoảng đã cho, số nào có nhiều hơn 2 ước số thì là hợp số.
Cách giải:
Số 5 có 2 ước số là số 1 và số 5. Do đó, số 5 là số nguyên tố.
Số 6 có 4 ước số là số 1, số 2, số 3 và số 6. Do đó, số 6 là hợp số.
Số 7 có 2 ước số là số 1 và số 7. Do đó, số 7 là số nguyên tố.
Số 8 có 4 ước số là số 1, số 2, số 4 và số 8. Do đó, số 8 là hợp số.
Số 9 có 3 ước số là số 1, số 3 và số 9. Do đó, số 9 là hợp số.
Số 10 có 4 ước số là số 1, số 2, số 5 và số 10. Do đó, số 10 là hợp số.
Như vậy, trong khoảng từ 5 đến 10 có 4 hợp số là số 6, số 8, số 9 và số 10.
5.5. Tìm bội chung nhỏ nhất (BCNN) và ước chung lớn nhất (ƯCLN)
Đề bài: Tìm BCNN và ƯCLN của số 9 và 12.
Phân tích đề bài:
Bội chung nhỏ nhất (BCNN): Phân tích hợp số thành thừa số nguyên số. BCNN là tích của các thừa số với số mũ lớn nhất.
Ước chung lớn nhất (ƯCLN): Phân tích hợp số thành thừa số nguyên số. ƯCLN là tích của các thừa số chung với số mũ nhỏ nhất.
Cách giải:
Phân tích số 9 thành thừa số nguyên tố: 9 = 3^2
Phân tích số 12 thành thừa số nguyên tố: 12 = 2^2 x 3
BCNN: Là tích của các thừa số chung và không chung với số mũ lớn nhất là 2^2 x 3^2 = 36.
ƯCLN: Là tích của các thừa số chung với số mũ nhỏ nhất là 3^1 = 3.
Như vậy, số 9 và số 12 có BCNN là 36 và ƯCLN là 3.
5.6. Bài toán thực tế liên quan đến hợp số
Đề bài: Một lớp có 20 học sinh. Giáo viên muốn chia lớp thành các nhóm có số học sinh bằng nhau và không còn dư. Vậy có bao nhiêu cách giải.
Cách giải:
Các ước số của 20 bao gồm: 1, 2, 4, 5, 10 và 20.
Như vậy, giáo viên có thể chia lớp thành các nhóm có 1, 2, 4, 5, 10 và 20 học sinh đều nhau.
Với giải đáp hợp số là gì, bài viết trên đã giúp bạn hiểu rõ về khái niệm này cũng như cách ứng dụng trong học tập và thực tiễn. Hy vọng những bài toán trong bài viết sẽ hữu ích với bạn!
Xem thêm: Bảng số La Mã từ 1 đến 100: Cách viết, đọc và ghi nhớ siêu dễCỰC HOT!!! Trang Công Nghệ có chương trình khuyến mãi giảm giá sâu đến 50% cho các sản phẩm nội thất, đồ gia dụng, điện tử,... cùng nhiều quà tặng hấp dẫn. Hơn nữa, khách hàng còn có cơ hội mua hàng trả góp 0% lãi suất, trả trước 0 đồng qua các công ty tài chính uy tín. Đội ngũ nhân viên luôn chăm sóc tận tình, tư vấn kỹ càng phù hợp với nhu cầu để bạn chọn được sản phẩm ưng ý nhất. Ngoài ra còn hỗ trợ khách hàng vận chuyển và lắp đặt miễn phí tại nhà, lỗi 1 đổi 1 trong 35 ngày đầu tiên,... |
















