Số nguyên tố là một khái niệm thú vị và rất quan trọng trong toán học được giảng dạy ở chương trình toán phổ thông của trung học. Đây là tiền đề để nâng cao thêm những kiến thức khác cho môn học. Vậy số nguyên tố là gì cũng như đặc điểm, tính chất và dãy số của nó ra sao, các bạn muốn tìm hiểu hãy xem ngay bài viết dưới đây nhé!
1. Số nguyên tố là gì?
Số nguyên tố là tập hợp các con số tự nhiên có giá trị lớn hơn 1, đồng thời chỉ chia được hết cho 1 và chính nó. Tức là ngoại trừ số 1 và nó ra thì khi thực hiện phép chia cho bất cứ số nào khác cũng đều có số dư theo dạng số thập phân. Số lượng các số nguyên tố là vô hạn và không thể thống kê được hết. Chúng bao gồm các số tiêu biểu như 2, 3, 5, 7, 13, 17, 23, 29….
2. Tính chất cơ bản của số nguyên tố
Dưới đây là những tính chất cơ bản của số nguyên tố để phân biệt với những con số khác:
Số nguyên tố không bao gồm số 1.
2 là số nguyên tố nhỏ nhất và cũng là số duy nhất chẵn.
Tất cả các con số nguyên tố đều không chia được hết cho 2, ngoại trừ số 2.
Số nguyên tố tương tự tập N bao gồm vô cực các con số, không có giới hạn.
Số nguyên tố chính là ước của 1 số bất kỳ thuộc tập N. Ví dụ 15 chia được hết cho các số 3 và 5 thì cả 3 và 5 đều là số nguyên tố.
Số X có ước nhỏ nhất là số dương khác 1 và nhỏ hơn căn bậc hai của X thì ước đó là số nguyên tố. Ví dụ ước nhỏ nhất của 30 là 5, trong đó 5 khác 1 và có giá trị thấp hơn căn bậc 2 của 30. Theo đó chúng ta có thể kết luận 5 là số nguyên tố.
3. Bảng số nguyên tố trong toán học chi tiết
Sau đây là bảng số nguyên tố chi tiết trong toán học có giá trị nhỏ hơn 1000:
2 | 47 | 109 | 191 | 269 | 353 | 439 | 523 | 617 | 709 | 811 | 907 |
3 | 53 | 113 | 193 | 271 | 359 | 443 | 541 | 619 | 719 | 821 | 911 |
5 | 59 | 127 | 197 | 277 | 367 | 449 | 547 | 631 | 727 | 823 | 919 |
7 | 61 | 131 | 199 | 281 | 373 | 457 | 557 | 641 | 733 | 827 | 929 |
11 | 67 | 137 | 211 | 283 | 379 | 461 | 563 | 643 | 739 | 829 | 937 |
13 | 71 | 139 | 223 | 293 | 383 | 463 | 569 | 647 | 743 | 839 | 941 |
17 | 73 | 149 | 227 | 307 | 389 | 467 | 571 | 653 | 751 | 853 | 947 |
19 | 79 | 151 | 229 | 311 | 397 | 479 | 577 | 659 | 757 | 857 | 953 |
23 | 83 | 157 | 233 | 313 | 401 | 487 | 587 | 661 | 761 | 859 | 967 |
29 | 89 | 163 | 239 | 317 | 409 | 491 | 593 | 673 | 769 | 863 | 971 |
31 | 97 | 167 | 241 | 331 | 419 | 499 | 599 | 677 | 773 | 877 | 977 |
37 | 101 | 173 | 251 | 337 | 421 | 503 | 601 | 683 | 787 | 881 | 983 |
41 | 103 | 179 | 257 | 347 | 431 | 509 | 607 | 691 | 797 | 883 | 991 |
43 | 107 | 181 | 263 | 349 | 433 | 521 | 613 | 701 | 809 | 887 | 997 |
4. Hướng dẫn phương pháp tìm số nguyên tố
Để tìm số nguyên tố, bạn có thể áp dụng theo 3 cách sau:
4.1. Cách 1: Tìm số nguyên tố A trong khoảng từ 2 đến (A – 1)
Nếu có số A trong khoảng từ 2 đến (A – 1), ta có thể tiến hành tìm số nguyên tố như sau:
Nếu A < 2: A không phải là số nguyên tố.
Nếu A > 2: Trong khoảng từ 2 đến (A - 1) không có ước số của A thì A chính là số nguyên tố.
Ví dụ: A = 17, trong khoảng từ 2 đến 16 không có ước số của 17 nên 17 là số nguyên tố.
4.2. Cách 2: Tìm số nguyên tố A trong khoảng từ 2 đến (A – 2)
Trong khoảng từ 2 đến (A – 2), ta có thể tìm được số nguyên tố A bằng cách xác định các số lẻ trong tập hợp. Nếu A không chia được hết cho bất cứ số nào thì A chính là số nguyên tố.
Ví dụ: A = 17, trong khoảng từ 2 đến 15 bao gồm các số lẻ là 3, 5, 7, 9, 13, 15. Tuy nhiên 17 không chia hết được cho bất cứ số lẻ nào trong đó nên 17 là số nguyên tố.
4.3. Cách 3: Sử dụng máy tính cầm tay để tìm số nguyên tố
Thông qua một chiếc máy tính cầm tay, bạn có thể dễ dàng tìm ra được số nguyên tố bằng thao tác: Nhập “A”, nhấn “=” rồi bấm tổ hợp “Shift + FACT”. Sau đó bạn sẽ đánh giá kết quả như sau:
Nếu kết quả ra A thì A là số nguyên tố.
Nếu kết quả trả về một phép nhân bất kỳ thì A không phải là số nguyên tố.
5. Một số dạng bài tập về số nguyên tố và ví dụ chi tiết
Để củng cố kiến thức về số nguyên tố, bạn hãy tham khảo những dạng bài tập cụ thể sau đây:
5.1. Dạng bài phân tích thừa số nguyên tố
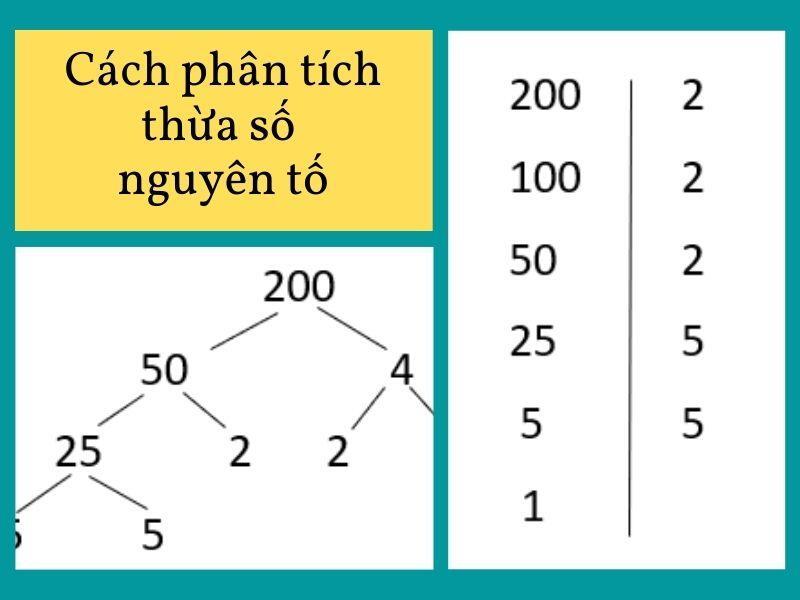
Phân tích thừa số nguyên tố là việc lấy số cần phân tích chia cho số nguyên tố nhỏ nhất có thể để tìm ra số nguyên tố cuối cùng. Bạn sẽ phải bắt đầu xem con số đó có chia được cho 2 không, nếu không sẽ xét tiếp tới các số 3, 5, 7 tới khi được một số chỉ chia được cho 1 và chính nó. Sau đó bạn lấy tất cả các thừa số tìm được nhân với nhau.
Ví dụ 1: Phân tích số 88 ra thừa số nguyên tố.
Với đề bài là số 88, ta lấy 88 : 2 = 44, số 44 : 2 = 22, số 22 : 2 = 11. Cuối cùng 11 chỉ chia được cho 1 và chính nó. Từ đó kết luận thừa số nguyên tố của 88 = 2 x 2 x 2 x 11.
Ví dụ 2: Phân tích thừa số nguyên tố với số 200.
Khi đề bài yêu cầu phân tích thừa số nguyên tố của 200, bạn hãy tiến hành như sau: lấy 200 : 2 = 100, 100 : 2 = 50, 50 : 2 = 25, đến số 25 không thể chia hết cho 2 được nữa nhưng có thể chia hết cho 5 và ra kết quả là 5. Tới 5 thì chỉ chia được cho 1 và chính nó. Vì thế thừa số nguyên tố của 200 = 2 x 2 x 2 x 5 x 5.
5.2. Dạng bài tìm ước số chung lớn nhất
Khi tìm hiểu số nguyên tố là gì chúng ta cũng thường thấy dạng bài tập tìm ước chung lớn nhất. Trong đó, đề bài có thể cho 1 số A và B có nhiều ước chung với nhau và bạn cần phải đi tìm ước số lớn nhất trong đó. Để tìm ra kết quả, bạn chỉ cần phân tích từng số ra thừa số nguyên tố của nó, sau đó nhân các thừa số nguyên tố chung với số mũ nhỏ nhất xuất hiện.
Ví dụ 1: Tìm ước chung lớn nhất của 2 số 50 và 80.
Ta tiến hành phân tích thừa số nguyên tố của cả 2 số sẽ ra kết quả như sau: 50 = 2 x 5 x 5 và 80 = 2 x 2 x 2 x 2 x 5.
Nhìn vào kết quả ta thấy 50 và 80 có thừa số chung là 2 và 5. Trong đó số mũ nhỏ nhất của 2 số này đều là 1 nên ước chung lớn nhất sẽ là 2 x 5 = 10.
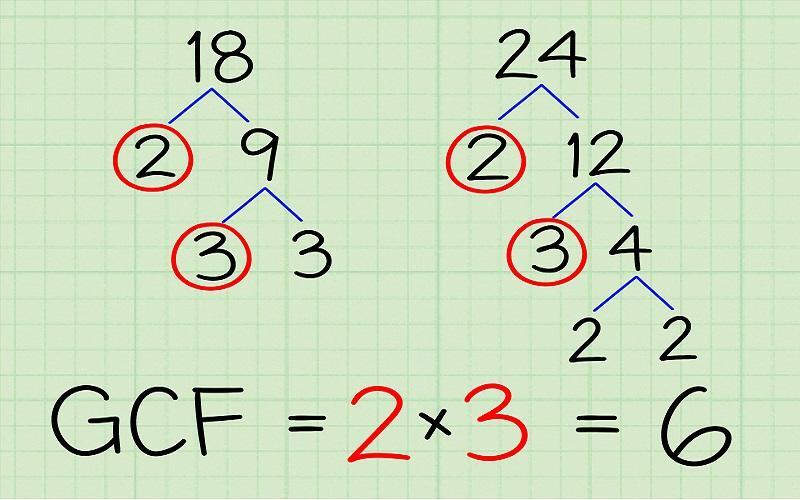
Ví dụ 2: Xác định ước chung lớn nhất của số 18 và 30.
Bước 1: Phân tích thừa số nguyên tố: 18 = 2 x 3 x 3, 30 = 2 x 3 x 5.
Bước 2: Tìm thừa số nguyên tố chung của 18 và 30 là 2 và 3 với số mũ nhỏ nhất là 1. Suy ra ước chung lớn nhất của 2 số này là 2 x 3 = 6.
6. Những thuật ngữ gắn liền với số nguyên tố
Bên cạnh khái niệm số nguyên tố, các bạn còn có thể gặp những thuật ngữ đi kèm là:
6.1. Số nguyên tố cùng nhau
2 số a và b được gọi là số nguyên tố cùng nhau nếu ước chung lớn nhất của cả a và b đều là 1.
Ví dụ: Số 3 và số 5 được gọi là số nguyên tố cùng nhau bởi ước chung lớn nhất của hai số này là 1.
6.2. Số siêu nguyên tố
Số siêu nguyên tố là một con số không bị thay đổi bản chất ngay cả khi thêm hoặc bớt số đi.
Ví dụ: Số 37 là một số siêu nguyên tố bởi khi bớt đi 7 hoặc 3 thì nó vẫn là một số nguyên tố. Ngược lại nếu bạn thêm số 3 hay 7 vào đằng trước hoặc đằng sau thành 337, 373, 773 thì bản chất số nguyên tố vẫn được giữ nguyên.
6.3. Tích các thừa số nguyên tố
Tích các thừa số nguyên tố chính là phép nhân thực hiện giữa các số nguyên tố bất kỳ.
Ví dụ: 3 x 5 = 15 hay 2 x 3 x 5 = 30.
Xem thêm: Bảng số La Mã từ 1 đến 100: Cách viết, đọc và ghi nhớ siêu dễBài viết trên đây đã giúp bạn giải đáp các thông tin số nguyên tố là gì cũng như tình chất và cách tìm chính xác. Hy vọng sau khi tham khảo, bạn có thể ứng dụng kiến thức để giải bài toán liên quan một cách chính xác và nhanh chóng nhé!
Để giúp các bạn học sinh dễ dàng tra cứu tài liệu để học tập, Siêu Thị Điện Máy - Nội Thất Chợ Lớn cung cấp đa dòng thiết bị điện thoại di động, máy tính bảng 100% chính hãng từ Apple, Samsung, Xiaomi, Oppo,... Các sản phẩm đều sở hữu hiệu năng mạnh mẽ, lượng pin ‘khủng’, màn hình sắc nét,... với mức giá đa dạng từ bình dân đến cao cấp. Nên phụ huynh dễ dàng lựa chọn thiết bị phù hợp nhu cầu và tài chính cho con.
Bên cạnh đó, Trang Công Nghệ còn cung cấp dịch vụ giao hàng tận nơi, chính sách bảo hành đáng tin cậy, hỗ trợ trả góp 0% lãi suất, hoàn chênh lệch nếu có siêu thị bán rẻ hơn,... Vậy nên, phụ huynh hãy đến ngay chi nhánh Siêu thị Điện Máy Nội Thất Chợ Lớn (xem địa chỉ gần nhất) hoặc liên hệ website chính thức: https://dienmaycholon.com/ để tham khảo và đặt hàng ngay nhé!
