Hình trụ là hình học không gian thú vị và có ứng dụng đa dạng trong cuộc sống hằng ngày. Tuy nhiên, không phải ai cũng hiểu rõ về tính chất và cách tính diện tích toàn phần hình trụ. Xem ngay bài viết dưới đây để được bật mí tường tận về hình trụ và các công thức toán học liên quan!
1. Hình trụ là hình gì?
Trong hình học không gian 3D, hình trụ là hình có giới hạn bởi hai đường tròn đường kính bằng nhau, kết nối bởi một mặt trụ.
Sách giáo khoa Toán lớp 9 định nghĩa: “Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.”
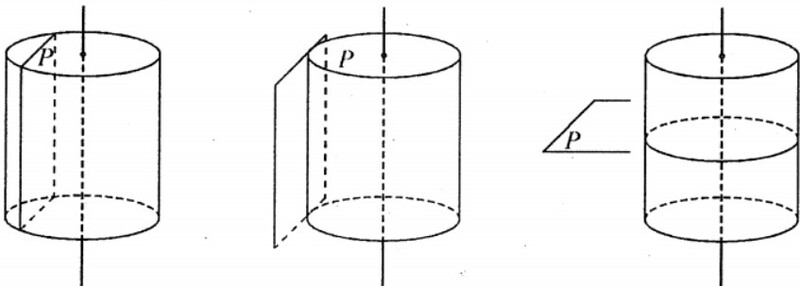
2. Tính chất của hình trụ
Các tính chất của hình trụ giúp bạn nhận diện hình học này một cách dễ dàng:
Hai mặt đáy của hình trụ là hình tròn có đường kính bằng nhau.
Hai cạnh nối từ hai đáy của hình trụ bằng nhau nếu song song với nhau.
Đường nối 2 tâm của mặt đáy gọi là trục tọa độ của hình trụ.
Các đường thẳng có chiều dài bằng trục tọa độ và song song với trụ này được gọi là các đường sinh.
3. Công thức tính diện tích hình trụ
Hình trụ được tạo thành bởi 2 đáy tròn bằng và song song nhau. Do đó, bạn dựa vào công thức tính diện tích và chu vi hình tròn để tính diện tích đáy, diện tích xung quanh và tổng diện tích toàn phần hình trụ.
3.1. Công thức tính diện tích xung quanh hình trụ
Diện tích xung quanh hình trụ là phần diện tích bề mặt bao xung quanh hình trụ mà không bao gồm 2 mặt đáy tròn. Muốn tính phần diện tích bề mặt xung quanh chỉ cần tính chu vi đường tròn mặt đáy và nhân với chiều cao hình trụ.
A = 2πrh |
Trong đó:
A: Diện tích xung quanh hình trụ.
2πr: Chu vi đường tròn mặt đáy. π = 3.14, r là độ dài bán kính hình tròn.
h: Độ dài chiều cao của hình trụ.
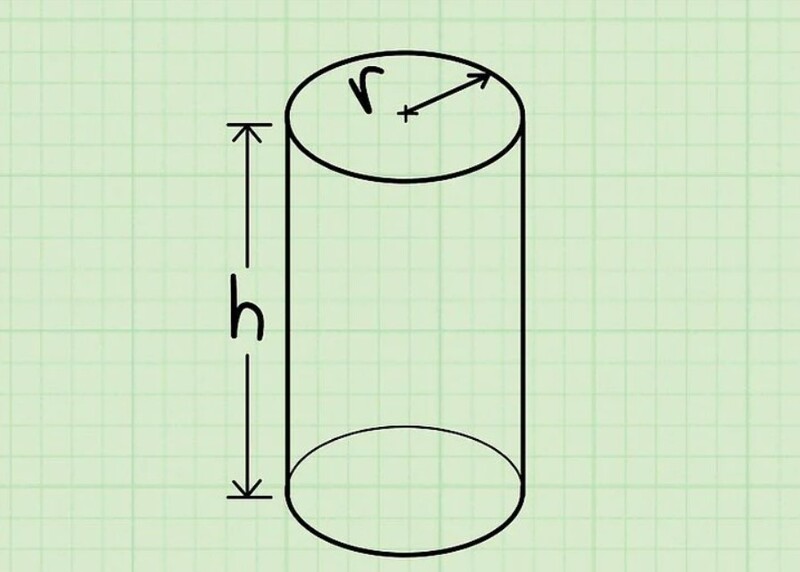
3.2. Công thức tính diện tích 2 đường tròn đáy
Hình trụ được tạo thành bởi 2 mặt đáy là 2 hình tròn bằng nhau. Công thức tính diện tích đường tròn đáy được áp dụng như sau:
B = 2πr² |
Trong đó:
B: Diện tích mặt đáy hình trụ.
π = 3.14
r: Độ dài bán kính hình tròn.
3.3. Cách tính diện tích toàn phần hình trụ
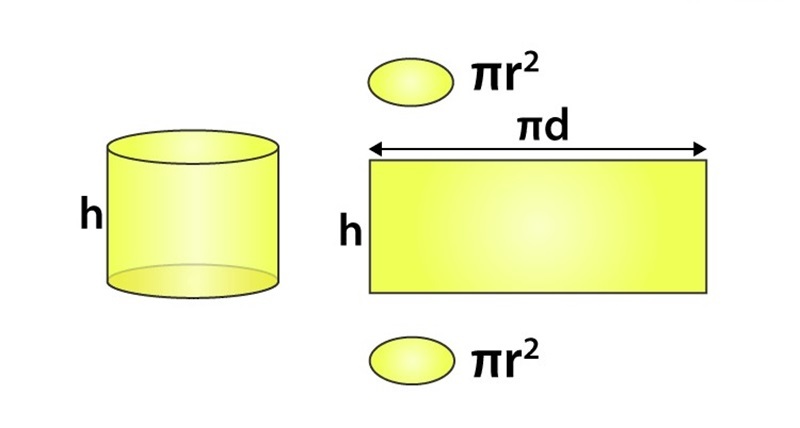
Tổng diện tích toàn phần hình trụ sẽ gồm diện tích bề mặt xung quanh và diện tích 2 mặt đáy tròn. Bạn chỉ cần cộng diện tích xung quanh với diện tích của 2 đáy sẽ ra kết quả:
S = 2πr² + 2πrh = 2πr(r + h) |
Trong đó:
h: Độ dài chiều cao của hình trụ.
π = 3.14
r: Độ dài bán kính hình tròn.
Sau khi biết được công thức tính diện tích xung quanh hình trụ và diện tích đáy thì diện tích toàn phần cũng được tính dễ dàng. Ví dụ minh họa dưới đây sẽ giúp mọi người ôn luyện công thức:
Ví dụ: Cho hình trụ có các số đo chiều cao 10cm, bán kính đáy 5cm. Hãy tính diện tích toàn phần của hình trụ.
Lời giải:
Diện tích xung quanh hình trụ là:
A = 2πrh = 2 x 3.14 x 5 x 10 = 314 cm2
Diện tích mặt đáy của hình trụ là:
B= 2πr² = 2 x 3.14 x 52 = 147 cm2
Diện tích toàn phần hình trụ là:
S = A + B = 314 + 147 = 471 cm2
Vậy diện tích của hình trụ là 471 cm2
Xem thêm: Công thức tính diện tích hình vuông chính xác, có ví dụ chi tiết4. Hướng dẫn cách tính thể tích hình trụ
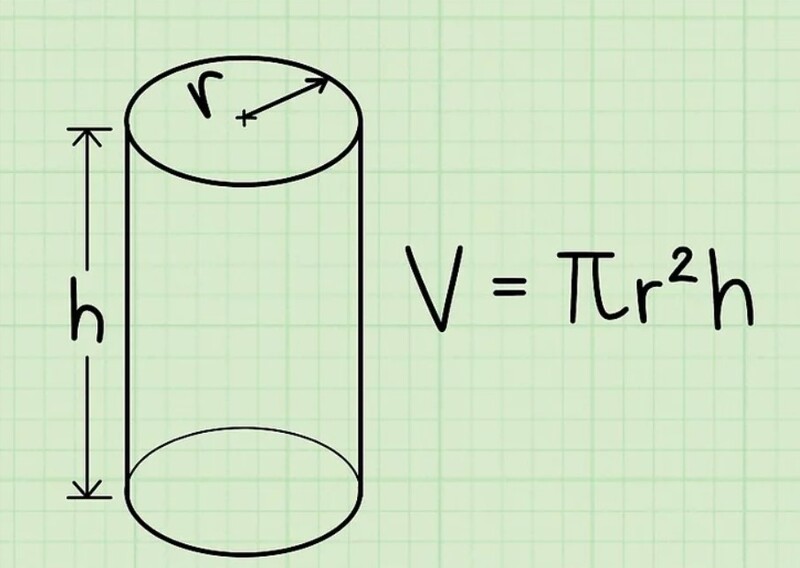
Bên cạnh diện tích hình trụ thì công thức tính thể tích hình trụ cũng là kiến thức quan trọng cần nắm. Cách tính thể tích hình trụ rất đơn giản bằng diện tích đáy nhân chiều cao:
V = 2πr²h |
Trong đó:
V: Thể tích của hình trụ.
π=3.14
r: Độ dài bán kính hình tròn.
h: Độ dài chiều cao của hình trụ.
Ví dụ: Cho hình trụ có chiều cao 10cm, bán kính 5cm. Tính thể tích của hình trụ.
Lời giải:
Thể tích của hình trụ là:
V = 2πr²h = 2 x 3.14 x 52 x 10 = 785 cm3
Đáp án: 785 cm3
5. Các dạng bài tập liên quan đến diện tích hình trụ
Các bài tập về hình trụ giúp bạn áp dụng công thức tính diện tích, thể tích hình trụ một cách linh hoạt.
5.1. Tính chiều cao hình trụ
Đề bài: Một hình trụ có diện tích xung quanh là 94.2 cm2 ; bán kính mặt đáy hình trụ là 3cm. Hãy tính chiều cao của hình trụ.
Lời giải:
Công thức tính diện tích xung quanh hình trụ: A = 2πrh
=> Chiều cao hình trụ là: h = A/2πr = A/(2 x 3.14 x 3) = 5 cm.
Vậy chiều cao của hình trụ là 5cm.
5.2. Tính bán kính đáy của hình trụ
Đề bài: Một hình trụ có diện tích bề mặt xung quanh là 125.6 cm2 . Độ dài chiều cao hình trụ là 4cm. Hãy tính bán kính của đáy tròn.
Lời giải:
Công thức tính diện tích xung quanh hình trụ: A = 2πrh
=> Bán kính của đáy tròn hình trụ là: r = A/2πh = 125.6/2 x 3.14 x 4 = 5cm.
Vậy bán kính đáy tròn có độ dài là 5cm.
5.3. Tính diện tích hình trụ khi biết đáy là đường tròn ngoại tiếp của tam giác
Đề bài: Một hình trụ có chiều cao h = 8cm, bán kính đáy hình tròn chính là bán kính của đường tròn ngoại tiếp tam giác ABC. Trong đó, độ dài các cạnh của tam giác ABC lần lượt là: a = 3cm, b = 4cm, c = 5cm. Hãy tính diện tích toàn phần của hình trụ.
Lời giải:
Bán kính của đường tròn ngoại tiếp tam giác ABC có độ dài là:
r=abc/√((a+b+c)(a+b−c)(a−b+c)(−a+b+c)) = 2.5cm
Diện tích toàn phần của hình trụ là:
S = 2πr(r + h) = 2 x 3.14 x 2.5(2.5 + 8) = 164.85 cm2
Vậy diện tích toàn phần của hình trụ là 164.85 cm2
5.4. Tính diện tích hình trụ khi biết đáy là đường tròn nội tiếp của tam giác
Đề bài: Cho tam giác ABC có độ dài các cạnh lần lượt là a = 3cm, b = 4cm, c = 5cm. Diện tích tam giác là 6cm2. Đường tròn nội tiếp của tam giác ABC chính là đáy của hình trụ có chiều cao là 8cm. Hỏi diện tích xung quanh của hình trụ là bao nhiêu?
Lời giải:
Độ dài bán kính đường tròn nội tiếp tam giác ABC là:
r = S/((a+b+c)/2) = 6/ ((3 + 4 + 5)/2) = 1cm.
Diện tích xung quanh hình trụ là:
S = 2πrh = 2 x 3.14 x 1 x 8 = 50.24 cm2
Vậy, diện tích xung quanh hình trụ là 50.24 cm2
Xem thêm: Công thức tính chu vi hình tròn dễ hiểu, có ví dụ chi tiết6. Một số ứng dụng phổ biến của hình trụ trong đời sống
Trong đời sống, các chuyên gia dành nhiều lời khen cho hình trụ bởi nhiều đặc tính nổi trội như: Chịu lực tốt, lưu trữ không gian tốt hơn nhiều hình không gian khác. Do đó, chúng ta dễ dàng bắt gặp các thiết kế ống khói, ống nước, cột trụ, các lon nước ngọt có hình trụ đứng.

Hy vọng bài chia sẻ trên đây đã giúp bạn đọc có thêm kiến thức về hình trụ và cách tính diện tích toàn phần hình trụ đơn giản. Đừng quên truy cập trang mỗi ngày để không bỏ lỡ thông tin hữu ích!
Trang Công Nghệ - Khuyến mãi cực khủng!!! Trang Công Nghệ hiện đang có nhiều chương trình ưu đãi cho các dòng điện thoại, máy tính bảng và đồ nội thất, gia dụng, mang đến cơ hội mua sắm thả ga không lo về giá cho khách hàng. Hơn nữa, siêu thị cam kết tất cả sản phẩm đều có mức giá cạnh tranh nhất thị trường, luôn cập nhật mẫu mã mới nhất, đa dạng sự lựa chọn. Đồng thời, Trang Công Nghệ còn hỗ trợ trả góp 0% lãi suất - trả trước 0 đồng, đổi trả 1-1 trong vòng 35 ngày đầu tiên nếu do lỗi kỹ thuật,... Cùng với đó là sự quan tâm, chăm sóc tận tâm chu đáo của đội ngũ nhân viên, giúp bạn lựa chọn được sản phẩm phù hợp nhất. > Ghé ngay Trang Công Nghệ (tra cứu địa chỉ tại đây) để trải nghiệm và rinh về những sản phẩm công nghệ, nội thất mới nhất với nhiều quà tặng hấp dẫn. |